Quadratic growth
For other uses of the word "quadratic" in mathematics, see Quadratic (disambiguation).
In mathematics, a function or sequence is said to exhibit quadratic growth when its values are proportional to the square of the function argument or sequence position, in the limit as the argument or sequence position goes to infinity. That is, in big Theta notation, 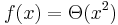 .
.
Examples of quadratic growth include
- Any quadratic polynomial.
- Certain integer sequences such as the triangular numbers. The nth triangular number has value n(n+1)/2, approximately n2/2.
- The amount of time taken in the worst case by certain algorithms, such as insertion sort, as a function of the input length.
- The numbers of live cells in space-filling cellular automaton patterns such as the Breeder (CA), as a function of the number of time steps for which the pattern is simulated.
- Metcalfe's law stating that the value of a communications network grows quadratically as a function of its number of users
Note:
In plain and simple English, quadratic growth is growth where the rate of change changes at a constant rate. For example, if you add 3 the first time, then you add 3.5 the next time, and 4 the time after that, that is quadratic growth. In this case, you added 0.5 to your rate of change each time.